學數學最好靠體系學習
學數學的最佳方式是體系學習,所謂體系學習,就是協助小朋友打穩根基,再進行符合小朋友程度的拓展,一步一步向上學習,根據認知規律去教導和引導學習,講求小朋友完全理解,而非一步登天,才能學好數學。今日 Jacky Sir會透過這篇文章,詳細講解小學學習中「 體系學習」之道。
- Jacky Sir讀小學的時候,每逢課堂上播放數學教育電視都會首先聽到一段全班同學很興奮的片頭曲:「一理通百明,白了計算可變簡單,全心探討數學,明道理答案終會找到 ~」一首歌就能帶領全班同學起認真學習,非常犀利!而隨著年紀增長,學習的經驗多了,就會發現這首歌除好聽裡面,更有著深層意義。
學數學要靠體系學習!
在教學的路途上, Jacky Sir遇過很多優秀的小學生,他們的學習能力非常強,在理解了最底層的邏輯後,往往能依靠自己能力作答題目 ,而Jacky Sir在黑板前解題的時候,他們往往能「自問自答」說出解題過程 ,這些有著自發學習能力的學生,他們學習之路是很快樂,而且學習效果非常之好,因為難題都是靠著自己的能力解出來的。
這就是體系學習的目的,根據認知規律去教導和引導學習,而非一步登天。透過學習知識點最底層的邏輯,一步一步引發小朋友思考出解題方法,以加強小朋友思考、理解、解難能力及對知識掌握的完整性。這種學習方法不但能打穩小朋友對已學知識的掌握程度,更能增強小朋友在學習途中的成功感,從而提升對學習興趣,並讓小朋友更自發地學習,形成良性循環。
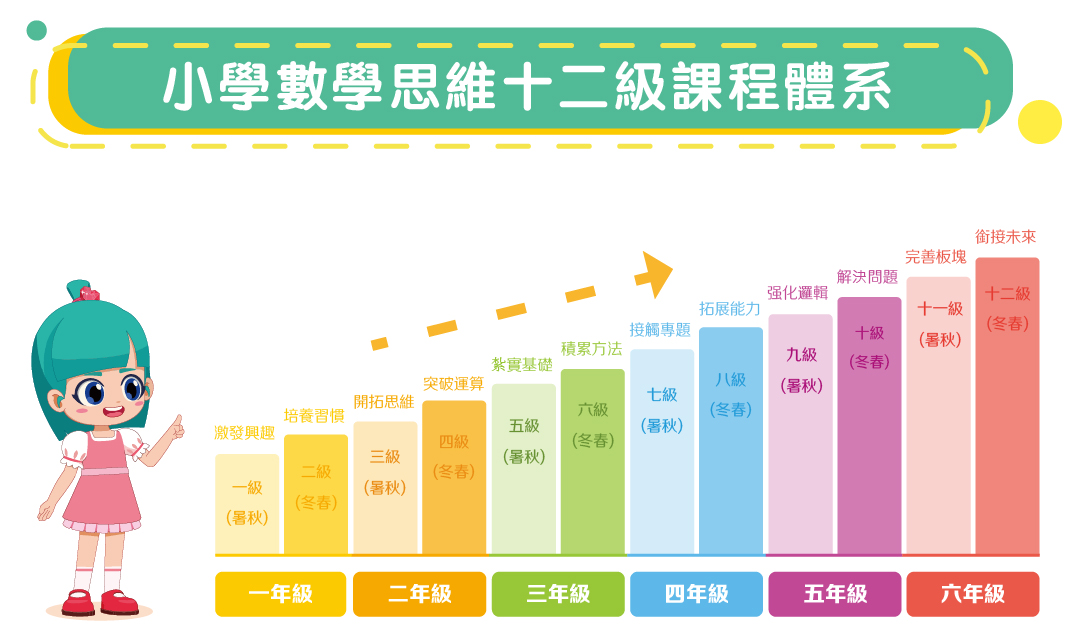
學數學為什麼要體系學習?
體系學習是著重給予小朋友成就感的方法, 根據小朋友的程度打通解題最關鍵的要點,再對小朋友進行適當引導。 但作為老師和家長,我們經常會用自己的視覺去看待小朋友正在學習知識, 常常把我們認為理所當然會懂的知識忽略,並只教小朋友如何用方法找到答案,卻沒有真正教會小朋友去理解 。
如果你想了解家長如何從旁協助小朋友學習,可以參考:學奧數為了「比賽獲獎」?它比你想像中有用得多!
以「列方程」這個知識點為例,很多家長教小朋友做數學比賽的應用題時,都會直接教自己認為是最容易的列方程解法,當然我們在真的理解方程概念時,用以解題真的既方便、又快捷。但對於小朋友來說,很多時只知道要把題目問的目標設為未知數 x,但對往後的列方程和解方程步驟毫無頭緒,遇到變型的題目時也根本無從入手,這情況不單出現在高年級,甚至有小朋友 3年級就用到二元、三方程去解和差倍應用難題,旁人看上肯定會覺得萬分厲害,但我們應該思考的是:小朋友真理解方程嗎?
我們常說知識是一棵樹,每個小朋友也有屬於自己知識樹,樹的根部延伸得越長,長出來的樹也越大越穩,所謂體系學習,就是協助小朋友打穩根基,再進行符合小朋友程度的拓展,一步一步向上學習,講求小朋友完全理解。以方程為例,方程是一項高階的概念,它要求小朋友對幾項前置知識有所認,包括
1) 未知數概念:需要先學習等量代換、字母表示數等知識;
2) 文字理解能力:需要先學習和差倍綜合、年齡問題、盈虧問題等知識 ;
3) 解方程的方法:需要先學習還原問題、算式還原、定義新運算等知識。
以上三點其實就是列方程解應用題的「設、列、解」三步曲,每一步都有其難題和重點知識,若當中有任何一步不清晰,小朋友都難以完整掌握方程的概念 。
我們可以說這些前置知識都是方程的根,打穩這些基礎再學就能讓小朋友學得更扎實,遇到不同類型的應用題時,也因過去已學過多種應用題的非方程解法而加深了對題目理解能力,從而更自如地運用方程解題。當然,方程也是很多後續知識的根,學好了也能對未來的數學學習有極大幫助。
其實不止是方程,每項知識也有其前置知識和後續知識,只有學得連貫才能紮打穩紮地拓展以前學過的知識,及為未來學習進階知識時做好準備。
所以, 若要提升小朋友的學習效果,我們需根據認知規律去教導和引導學習, 對比於「硬塞」知識式的教學,體系學習為小朋友提供了學習階梯,協助小朋友完善、有體系地學好數學知識,大大強化所有知識的連貫性。
相關文章:
