小四數學考試難題大拆解 ── 五分鐘解讀因倍數理論
小四的家長,你可有發覺時光飛逝,仿佛才剛與小朋友迎來小四的開學日,喘息未定,現已臨近小朋友高小階段的一個測驗考試季節。根據Google Trend的分析,從9月2日開始在Google搜尋因數及倍數的人數急速上升。作為小四家長的你可有發覺因倍數這個理論很熟悉?熟悉是因為在剛過去的一個月,你每日每夜都為小朋友向Google大神請教因倍數相關知識?倘若我在此告訴你,你只要花五分鐘把下文都讀完,就能夠結束你那漫長的Google搜尋因倍數之夜,你可願意花這五分鐘?
撰文:Lawson Sir
剛剛提到,在剛過去的九月份在Google搜尋因倍數的人次達到高峰,而我作為學而思小學四年級的數學思維訓練導師,對此結果並不感詫異。因為,因倍數等理論所屬的數學版塊是小朋友在初小階段從未接觸過的「數論板塊」。而「數論板塊」是小朋友到四年級才首次接觸的板塊,所以對小朋友而言「數論板塊」中的因倍數理論是十分陌生難明的。

一、概念講解
1、因數與倍數
如果a(a不能是0) 可以整除 b(即 b÷a 沒有餘數),那麼a就是b的因數,b就是a的倍數。(例如:6÷3=2,6是3的倍數,3是6的因數)
所以在同一條算式中,倍數一般是較大數,而因數一般是較小數
2、公因數與公倍數
如果 a 是 b 的因數,也是c 的因數,那麼a 就是 b和c 公共的因數,稱為公因數。(例如:2是4的因數,2也是6的因數,那麼2就是4和6的公因數)
如果 a是 b的倍數,也是c的倍數,那麼a就是是 b和c 公共的倍數,稱為公倍數。(例如:12是3的倍數,12也是4的倍數,那麼12就是3和4的公倍數)
3、最大公因數與最小公倍數
公因數中的最大數稱為最大公因數,公倍數中的最小數稱為最小公倍數。
對於公因數,我們會研究最大公因數(即HCF)。因為最小公因數人人都知道,就是1。
對於公倍數,我們會研究最小公倍數(即LCM)。因為最大公倍數無窮無盡,其數值之大,是小朋友和我們這些大人難以想像的。

二、解題方法
1、求一個數的所有因數或倍數
枚舉法(也就是列舉法)是最為普遍能夠求得一個數所有因數的方法。而枚舉法相對四年級其他理論簡單直接易明,相信大部分小朋友都已經熟知如何操作。如果小朋友乘數表記得比較牢固,用枚舉法求所有因數或倍數的題型將不會難倒他們。
如果小朋友在用枚舉法做題時確實感到有難度,我建議小朋友多做乘除法的計算,提升基礎計算能力,將枚舉法的基本──乘除法練好,相信到時候小朋友就能輕鬆使用枚舉法列舉所有因數或倍數了。
2、求最大公因數(HCF)與最小公倍數(LCM)的方法
①枚舉法
最大公因數:將兩個數的所有因數列舉出來,選取公共因數中最大的一個即可。
最小公倍數:將兩個數的倍數盡量列舉出來,直到出現公共倍數。選取公共倍數中最小的一個即可。
②短除法
相信大家都在學校學習過短除法,所以我和大家講講短除法的技巧。
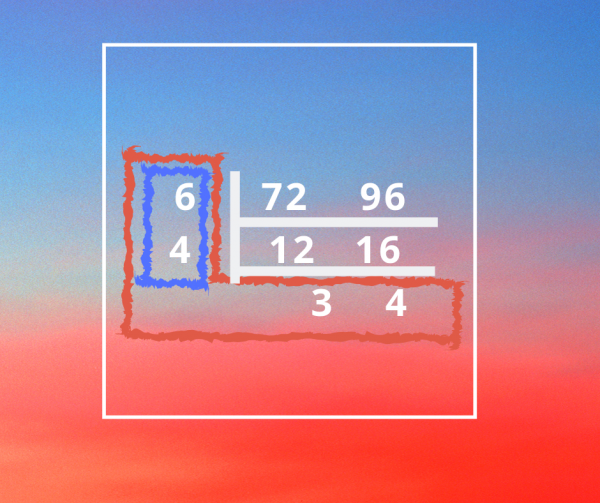
以「求72和96的HCF、LCM」為例。
第一步:
我們用短除法,一直除到「商」互質,即3和4沒有共同的因數。
(商即是被除數除以除數得出的結果)
(互質即兩個沒有1以外的公因數的數)
第二步:
使用以下口訣:最大公因乘左邊(藍色部分),最小公倍乘半圈(紅色部分)。
即HCF=6×4=24;LCM=6×4×3×4=288。
小技巧:
最小公倍即LCM,剛好紅色部分就好像L,所以倘若小朋友還是記不住如何使用短除法取得最小公倍數,家長可以使用圖像法,教小朋友LCM就是將短除直式中L的部分相乘。
三、大因小倍的規律
1、當兩數互質(兩數互質即兩數的公因數只有1)。他們的HCF為1,他們的LCM為兩數的乘積(乘積即是兩個數相乘出來的結果)。
以「求7和8的HCF、LCM」舉例。由於7和8互質,所以7和8的HCF為1,7和8的LCM為7×8, 即是56。
2、當兩數為倍數關係。他們的HCF為較小數,他們的LCM為較大數。
以「求4和8的HCF、LCM」舉例。由於4和8為倍數關係,所以4和8的HCF為4,4和8的LCM為8。
五分鐘剛好過去,這篇文是否仿佛幫你把因倍數的神秘面紗揭開一樣?你是否瞬間覺得原來因倍數是能夠如此簡單易明的?
把文章都看畢后,大家可以看看我在早前錄影講解有關於因倍數理論的視頻,沉澱及梳理一下從文章學到的因倍數理論知識。
點擊觀看小四因倍數理論講解視頻
加入數學思維訓練Whatsapp群
為小朋友提升數學思維能力
最後,倘若小朋友在因倍數理論這個課題中能夠輕鬆明白當中奧妙,家長希望提升小朋友的數學思維能力,或者家長想和我Lawson Sir討論更多數學問題,歡迎加入學而思的數學思維訓練群組。
